Welcome







The research and teaching activities at our institute focus on geometry acquisition and processing, on interactive visualization, and on related areas such as computer vision, photo-realistic image synthesis, and ultra high speed multimedia data transmission.
In our projects we are cooperating with various industry companies as well as with academic research groups around the world. Results are published and presented at high-profile conferences and symposia. Additional funding sources, among others, are the Deutsche Forschungsgemeinschaft and the European Union.
News
| • |
We have a paper on greedily generating artwork using Bézier segments at VMV 2023. |
May 23, 2023 |
| • |
Our paper on surface maps received the Günter Enderle Best Paper Award at Eurographics 2023. |
May 12, 2023 |
| • |
We have a paper on the interactive segmentation of textured point clouds at VMV 2022. |
Oct. 4, 2022 |
| • |
Our paper on automatic differentiation received the best paper award (1st place) at the Symposium on Geometry Processing 2022 |
July 6, 2022 |
| • |
We have a paper on fast and exact mesh Booleans at SIGGRAPH 2022. |
June 13, 2022 |
| • |
In collaboration with CNIC Madrid we have a paper on the geometry of heart development in Nature Cardiovascular Research. |
May 18, 2022 |
Recent Publications
 Neural Implicit Shape Editing Using Boundary Sensitivity International Conference on Learning Representations 2023 Neural fields are receiving increased attention as a geometric representation due to their ability to compactly store detailed and smooth shapes and easily undergo topological changes. Compared to classic geometry representations, however, neural representations do not allow the user to exert intuitive control over the shape. Motivated by this, we leverage boundary sensitivity to express how perturbations in parameters move the shape boundary. This allows to interpret the effect of each learnable parameter and study achievable deformations. With this, we perform geometric editing: finding a parameter update that best approximates a globally prescribed deformation. Prescribing the deformation only locally allows the rest of the shape to change according to some prior, such as semantics or deformation rigidity. Our method is agnostic to the model its training and updates the NN in-place. Furthermore, we show how boundary sensitivity helps to optimize and constrain objectives (such as surface area and volume), which are difficult to compute without first converting to another representation, such as a mesh. 
|
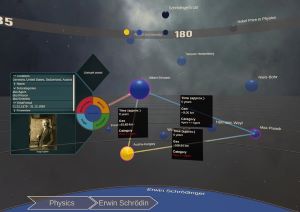 Who Did What When? Discovering Complex Historical Interrelations in Immersive Virtual Reality Konferenz: 2023 IEEE International Symposium on Mixed and Augmented Reality Traditional digital tools for exploring historical data mostly rely on conventional 2D visualizations, which often cannot reveal all relevant interrelationships between historical fragments (e.g., persons or events). In this paper, we present a novel interactive exploration tool for historical data in VR, which represents fragments as spheres in a 3D environment and arranges them around the user based on their temporal, geo, categorical and semantic similarity. Quantitative and qualitative results from a user study with 29 participants revealed that most participants considered the virtual space and the abstract fragment representation well-suited to explore historical data and to discover complex interrelationships. These results were particularly underlined by high usability scores in terms of attractiveness, stimulation, and novelty, while researching historical facts with our system did not impose unexpectedly high task loads. Additionally, the insights from our post-study interviews provided valuable suggestions for future developments to further expand the possibilities of our system. 
|
 Towards Discovering Meaningful Historical Relationships in Virtual Reality 2023 IEEE Conference on Virtual Reality and 3D User Interfaces Abstracts and Workshops (VRW) Traditional digital tools for exploring historical data mostly rely on conventional 2D visualizations, which often cannot reveal all relevant interrelationships between historical fragments. We are working on a novel interactive exploration tool for historical data in virtual reality, which arranges fragments in a 3D environment based on their temporal, spatial and categorical proximity to a reference fragment. In this poster, we report on an initial expert review of our approach, giving us valuable insights into the use cases and requirements that inform our further developments. 
|

