Research Areas
Research of the computer graphics group at RWTH Aachen focuses on geometry acquisition and processing, on interactive visualization, and on related areas such as computer vision, photo-realistic image synthesis, and ultra high speed multimedia data transmission.
In our projects we are cooperating with various industry companies as well as with academic research groups around the world. Additional funding sources are the Deutsche Forschungsgemeinschaft and the European Union.
This page presents some examples of our current research projects. If you are interested in one of the topics please contact us by email for further detail information or check out our publications page on which you can find papers, software, and additional material for download.

A common dilemma in todays CAM production environments are the different geometry representations that are employed by CAD systems on the one hand and downstream applications like computational fluid- or structure simulation, rapid prototyping, and numerically controlled machining on the other hand. The conversion between different representations creates artifacts like gaps, holes, intersections and overlaps which have to be removed in tedious and often manual post-processing steps.
We are focussing on the development of new algorithms to efficiently solve the model repair problem. Our hybrid approaches combine the advantages of traditional surface-oriented and volumetric algorithms. We exploit the topological simplicity of a voxel grid to reconstruct a cleaned up surface in the vicinity of intersections and cracks, but keep the input tessellation in regions that are away from these inconsistencies. We are thus able to preserve the characteristic structure of the input tessellation, close gaps up to a user-defined maximum diameter, resolve intersections, handle incompatible patch orientations and produce a feature-sensitive, manifold output that stays within a prescribed error-tolerance to the input model.
Also see our papers:
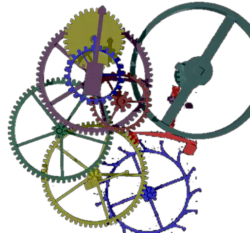
In many applications (prototyping and simulation, movies, games, ... ) the physically correct behavior of 3D objects is an improtant issue. This behavior should for example consider the dynamics of rigid bodies. Here objects can move through space, collide with each other and are liable to the laws of friction. Once one can simulate that, there is the possibility to add more degrees of freedom, e.g. object deformation by external and internal forces. With finite element methods these deformations can be handled in an efficient way. If we further increase the deformable character of the objects we may get materials like fluids or gases. Once all these phenomenas can be handled, a next step would be to simulate the interaction between all these different matters.
Our goal in this context one the one hand is to integrate as many of these physical effects as possible to gain maximum physical correctness and on the other hand we want do to this as fast as possible, i.e. in realtime. Clearly there is a tradeoff between these goals. Desirable are algorithms which cover the whole range of application whereas the tradeoff between efficiency and precision can be controlled by a simple parameter.

When modeling geometric objects it is important to be able to switch between different levels of resolution of the object: At one time one might want to create fine details, like the eyes of a character, another time the designer may want to change the overall shape of the object without losing these details. This problem requires a suitable internal representation of the object and algorithms that enable to switch between the various levels of detail. In fact a decomposition of the geometric shape into disjoint "frequency bands" is necessary (multiresolution representation). If the different levels of detail are defined relative to each other then we have a fully hierarchical representation of the underlying object.
Our research is focussing on algorithms that allow the designer to interactively edit a freeform object on arbitrary levels of resolution. Besides the underlying mathematical methods we are investigating new design metaphors to facilitate the handling of multiresolution surfaces within an interactive framework.

Subdivision schemes have become increasingly popular in recent years because they provide a simple and efficient construction of smooth curves and surfaces. In contrast to plain piecewise polynomial representations like Bezier patches and NURBS, subdivision schemes can easily represent smooth surfaces of arbitrary topology.
At our institute we are investigating the analysis of subdivision surfaces as well as their applications in geometric modeling and other computer graphics areas. We develop new subdivision schemes that accomodate specific requirements and carry over classical NURBS tools to subdivision surfaces.
Also see our papers:
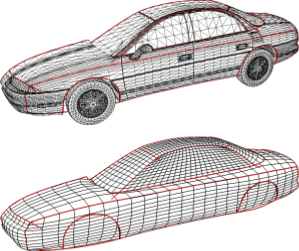
We present a novel approach to feature-aware mesh deformation. Previous mesh editing methods are based on an elastic deformation model and thus tend to uniformly distribute the distortion in a least squares sense over the entire deformation region. Recent results from image resizing, however, show that discrete local modifications like deleting or adding connected seams of image pixels in regions with low saliency lead to far superior preservation of local features compared to uniform scaling -- the image retargeting analogon to least squares mesh deformation. Hence, we propose a discrete mesh editing scheme that combines elastic as well as plastic deformation (in regions with little geometric detail) by transferring the concept of seam carving from image retargeting to the mesh deformation scenario. A geometry seam consists of a connected strip of triangles within the mesh's deformation region. By collapsing or splitting the interior edges of this strip we perform a deletion or insertion operation that is equivalent to image seam carving and can be interpreted as a local plastic deformation. We use a feature measure to rate the geometric saliency of each triangle in the mesh and a well-adjusted distortion measure to determine where the current mesh distortion asks for plastic deformations, i.e., for deletion or insertion of geometry seams. Precomputing a fixed set of low-saliency seams in the deformation region allows us to perform fast seam deletion and insertion operations in a predetermined order such that the local mesh modifications are properly restored when a mesh editing operation is (partially) undone. Geometry seam carving hence enables the deformation of a given mesh in a way that causes stronger distortion in homogeneous mesh regions while salient features are preserved much better.
Also see our papers:

Remeshing algorithms are fundamental for the generation of high-quality CAD models in rapid prototyping, reverse engineering and conceptual design. Traditionally, remeshing algorithms where focused on improving the local mesh characteristics, i.e., on generating mesh elements with optimal shape and regularity (nearly quadratic). Recently the focus has widened to also incorporate structural considerations, i.e. the alignment of the elements to mesh features like edges and corners. We propose a two-step approach: In a first step the model is segmented into a set of (almost) planar regions that capture the overall structure of the model. In the second step, these regions are remeshed while taking consisteny constraints along their abutting boundaries into account. This way we obtain a high-quality, quad-dominant remesh that properly reflects the features of the input model.
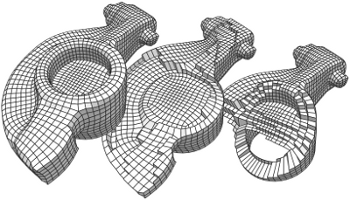
A purely topological approach for the generation of hexahedral meshes from quadrilateral surface meshes of genus zero has been proposed by M. Müller-Hannemann: in a first stage, the input surface mesh is reduced to a single hexahedron by successively eliminating loops from the dual graph of the quad mesh; in the second stage, the hexahedral mesh is constructed by extruding a layer of hexahedra for each dual loop from the first stage in reverse elimination order. In this paper, we introduce several techniques to extend the scope of target shapes of the approach and significantly improve the quality of the generated hexahedral meshes. While the original method can only handle "almost convex" objects and requires mesh surgery and remeshing in case of concave geometry, we propose a method to overcome this issue by introducing the notion of concave dual loops. Furthermore, we analyze and improve the heuristic to determine the elimination order for the dual loops such that the inordinate introduction of interior singular edges, i.e. edges of degree other than four in the hexahedral mesh, can be avoided in many cases.
Also see our paper:

In 3-axis CNC milling, excess material is removed slice by slice by a tool head from a solid block of material. A number of different strategies have been explored which generally try to optimize the tool-paths to achieve high throughput at low machine wear-off. Classical approaches for computing the tool-paths are plagued by various numerical problems that result in poor performance and complex program architectures.
We adopt an alternative approach that exploits the computing power of modern GPUs to achieve fast and robust algorithms. Our idea is to compute the signed distance field to a given contour and extract the tool-paths as isocurves of the field. This approach avoids the handling of special cases and leads to unprecedented speed when implemented in parallel on a graphics processor. Currently we are working on a generalization of these techniques to 5-axis machining.

Procedural modeling is a promising approach to create complex and detailed 3D objects and scenes. Based on the concept of split grammars, e.g., construction rules can be defined textually in order to describe a hierarchical build-up of a scene. Unfortunately, creating or even just reading such grammars can become very challenging for non-programmers. Recent approaches have demonstrated ideas to interactively control basic split operations for boxes, however, designers need to have a deep understanding of how to express a certain object by just using box splitting. Moreover, the degrees of freedom of a certain model are typically very high and thus the adjustment of parameters remains more or less a trial-and-error process. ...

In mechanical engineering and architecture, structural elements with low material consumption and high load-bearing capabilities are essential for light-weight and even self-supporting constructions. This paper deals with so called point-folding elements - non-planar, pyramidal panels, usually formed from thin metal sheets, which exploit the increased structural capabilities emerging from folds or creases. Given a triangulated free-form surface, a corresponding point-folding structure is a collection of pyramidal elements basing on the triangles. User-specified or material-induced geometric constraints often imply that each individual folding element has a different shape, leading to immense fabrication costs. We present a rationalization method for such structures which respects the prescribed aesthetic and production constraints and ?nds a minimal set of molds for the production process, leading to drastically reduced costs. For each base triangle we compute and parametrize the range of feasible folding elements that satisfy the given constraints within the allowed tolerances. Then we pose the rationalization task as a geometric intersection problem, which we solve so as to maximize the re-use of mold dies. Major challenges arise from the high precision requirements and the non-trivial parametrization of the search space. We evaluate our method on a number of practical examples where we achieve rationalization gains of more than 90%.
Also see our papers:

The computation of intrinsic, geodesic distances and geodesic paths on surfaces is a fundamental low-level building block in countless Computer Graphics and Geometry Processing applications. This demand led to the development of numerous algorithms – some for the exact, others for the approximative computation, some focussing on speed, others providing strict guarantees. Most of these methods are designed for computing distances according to the standard Riemannian metric induced by the surface’s embedding in Euclidean space. Generalization to other, especially anisotropic, metrics – which more recently gained interest in several application areas – is not rarely hampered by fundamental problems. We explore and discuss possibilities for the generalization and extension of well-known methods to the anisotropic case, evaluate their relative performance in terms of accuracy and speed, and propose a novel algorithm, the Short-Term Vector Dijkstra. This algorithm is strikingly simple to implement and proves to provide practical accuracy at a higher speed than generalized previous methods.

OpenMesh is a generic and efficient data structure for representing and manipulating polygonal meshes. It is funded by the German Ministry for Research and Education (BMBF).
It was designed with the following goals in mind :
- Flexibility : provide a basis for many different algorithms without the need for adaptation.
- Efficiency : maximize time efficiency while keeping memory usage as low as possible.
- Ease of use : wrap complex internal structure in an easy-to-use interface.
Also visit the OpenMesh Webpage and see our paper:

OpenVolumeMesh is a generic data structure for the comfortable handling of arbitrary polytopal meshes. Its concepts are closely related to OpenMesh. In particular, OpenVolumeMesh carries the general idea of storing edges as so-called (directed) half-edges over to the face definitions. So, faces are split up into so-called half-faces having opposing orientations. But unlike in the original concept of half-edges, local adjacency information is not stored on a per half-edge basis. Instead, all entities are arranged in arrays, which makes OpenVolumeMesh an index-based data structure where the access to entities via handles is accomplished in constant time complexity. By making the data structure index-based, we alleviate the major drawback of the half-edge data structure of only being capable to represent manifold meshes. In our concept, each entity of dimension n only stores an (ordered) tuple of handles (or indices) pointing to the incident entities of dimension (n-1). These incidence relations are called the top-down incidences. They are intrinsic to the implemented concept of volumentric meshes. One can additionally compute bottom-up incidences, which means that for each entity of dimension n, we also store handles to incident entities of dimension (n+1). These incidence relations have to be computed explicitly which can be performed in linear time complexity. Both incidence relations, the top-down and the bottom-up incidences, are used to provide a set of iterators and circulators that are comfortable in use. As in OpenMesh, OpenVolumeMesh provides an entirely generic underlying property system that allows attaching properties of any kind to the entities.
Also visit the OpenVolumeMesh Webpage and see our paper:
![]()
OpenFlipper is an OpenSource multi-platform application and programming framework designed for processing, modeling and rendering of geometric data. On the one hand OpenFlipper is an easy to use application for modifying and processing geometry. On the other hand OpenFlipper is a powerful framework allowing researchers to focus on their primary work and not having to write their own viewer or user interaction. OpenFlipper will work on Windows, MacOS X and Linux. We provide the same user interface and functionality on all platforms. Basic selection metaphors, a smoother, a decimater and many other algorithms are already included. As we make use of OpenMesh for our surface representation we support a variety of different file formats( off, obj, ply, ... ). For developers OpenFlipper provides a highly flexible interface for creating and testing own geometry processing algorithms. Basic functionality like rendering, selection and a lot of user interaction is provided by the system which significantly reduces the coding effort for developing new geometry processing algorithms. A scripting language can be used to access all parts of OpenFlipper and modify geometry or the user interface at runtime. This way developers can automatically test their algorithms with different parameters, take snapshots and compare the results just by using small scripts. Due to the multi platform system developers can reach a large group of users without having to change any line of code. OpenFlipper loads binary modules at runtime, so developers can easily hand out plugins without having to publish their source code.
Also visit the OpenFlipper Webpage and see our paper:


The faithful digitization and digital reproduction of three dimensional real world objects is one of the fundamental challenges in computer graphics and computer vision. Although established technologies such as laser scanning are able to produce high quality 3D reconstructions, they still lack flexibility with respect to material and lighting conditions, are relatively expensive, and are often applicable only to restricted types of objects.
In this research area we are focusing on new techniques to reconstruct 3D objects from simple photos or video. We investigate new solutions to involved problems such as camera calibration, structure from motion, and methods for volumetric and explicit surface reconstruction.
During the last years we have developed new techniques to efficiently solve two of the central questions in image-based reconstruction. Our highly efficient and illumination invariant photo-consistency measure for image-based, volumetric 3D reconstruction allows us to compute reliable probability estimates whether the desired object surface passes through a specific region in space or not. Furthermore, we presented new methods for surface extraction from such photo-consistency volumes, which allow us to generate triangle meshes that are faithful reproductions of the real 3D object surface solely from images.
We also showed that our solutions are applicable to a number of other, difficult 3D reconstruction problems such as unoriented point clouds.

Estimating the position and orientation of a camera given an image taken by it is an important step in many interesting applications such as tourist navigations, robotics, augmented reality and incremental Structure-from-Motion reconstruction. To do so, we have to find correspondences between structures seen in the image and a 3D representation of the scene. Due to the recent advances in the field of Structure-from-Motion it is now possible to reconstruct large scenes up to the level of an entire city in very little time. We can use these results to enable image-based localization of a camera (and its user) on a large scale. However, when processing such large data, the computation of correspondences between points in the image and points in the model quickly becomes the bottleneck of the localization pipeline. Therefore, it is extremely important to develop methods that are able to effectively and efficiently handle such large environments and that scale well to even larger scenes.
Also visit the Image-Based Localization project page and see our papers:


Digital watermarking techniques as they are known from classical media like images, videos and sound become more and more important in geometric models to enable copyright protection and ownership verification. In particular, the widely used spread-spectrum methods can be generalized to 3D datasets but are often far too slow to cope with very large meshes due to their complex computations.
We explore alternative spectral watermarking schemes that are based on orthogonalized radial basis functions. Our algorithm achieves high resistance against various real-world attacks but even more importantly, it runs faster by two orders of magnitude and thus can efficiently watermark even very large models.
Also see our paper:

Table display surfaces, like Microsoft PixelSense, can display multimedia content to a group of users simultaneously, but it is expensive and lacks mobility. On the contrary, mobile devices are more easily available, but due to limited screen size and resolution, they are not suitable for sharing multimedia data interactively. In this paper we present a "Dynamic Tiling Display", an interactive display surface built from mobile devices. Our framework utilizes the integrated front facing camera of mobile devices to estimate the relative pose of multiple mobile screens arbitrarily placed on a table. Using this framework, users can create a large virtual display where multiple users can explore multimedia data interactively through separate windows (mobile screens). The major technical challenge is the calibration of individual displays, which is solved by visual object recognition using front facing camera inputs.
Also see our papers:


Because of their conceptual simplicity and superior flexibility, point-based geometries evolved into a valuable alternative to surface representations based on polygonal meshes. In particular elliptical surface splats were shown to allow for high-quality anti-aliased rendering by sophisticated EWA filtering. Our research focuses on improving the efficiency and visual quality of these algorithms in two ways: First, we leverage as much as possible of the involved computations to the GPU which allows us to generate high-quality, anti-aliased and dynamically shaded visualizations at a rate of of more than 20M elliptical splats per second. Second, we impose a hierarchical structure on the set of input points that allows us to adapt the object complexity to the requirements and features of the target hardware in a multi-resolution approach.
Also see our papers:


Using global illumination techniques, we are able to generate photorealistic images and movie sequences. This is important in areas of visualization, architecture, advertisement, movies and video games. Both offline and real-time rendering are of interest, and we in particular focus on real-time global illumination which can be used to create even more convincing video games and a stunning virtual reality for the user.
Also see our paper:
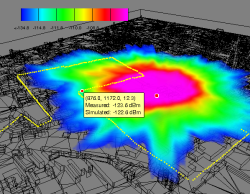
Global illumination can also be applied to compute the propagation of radio waves, e.g. in buildings or urban environments. This is for example important in the context of wireless networks or mobile phone networks. Predicting reception quality of mobile nodes and simulation of mobile networks is a hot topic in the network computing community. With the knowledge gained from the image synthesis aspects of global illumination, we are able to create accurate and physics based solutions to the wave propagation problem.


If the processing of digital images is supposed to go beyond mere filtering, one of the most basic operations is to add or remove objects from a given image. While adding an object to the foreground of an image is comparably easy (if we ignore relighting issues), removing an object is usually quite difficult because the now-visible background has to be reconstructed properly in order to hide the modification to the viewer.
Besides image completion approaches that are based on filtering or texture-synthesis, the fragment-based approaches have been shown to lead to the most convincing results. In these approaches the image regions, where foreground objects have been removed, are filled by iteratively copying small patches (source fragments) of the input image to the boundary of the unknown region (target fragment) until they completely cover the unknown region.
We have developed a new approach for computing fragment-based image completion which enables its integration into an interactive inpainting tool.
Also see our paper:

In recent years, research on two-dimensional image manipulation has received a huge amount of interest. Very powerful solutions for problems such as matting, image completion, texture synthesis, or rigid image manipulation have been presented. Based on these and similar methods it has now become possible to explore interesting new ideas to re-animate still pictures.
In this project we want to take the idea of creating animations directly in image space one step further by making photographed persons move. We developed a purely image based approach to combine real images with real 3D motion data in order to generate visually convincing animations of 2D characters from only a single image.
For animated Videos and the corresponding paper, see also:

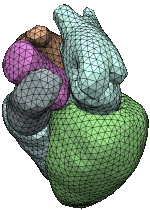
Extracting isosurfaces from volumetric datasets is an essential step for indirect volume rendering algorithms. For physically measured data like it is used, e.g. in medical imaging applications one often introduces topological errors such as small handles that stem from measurement inaccuracy and cavities that are generated by tight folds of an organ. During isosurface extraction these measurement errors result in a surface whose genus is much higher than that of the actual surface. In many cases however, the topological type of the object under consideration is known beforehand, e.g., the cortex of a human brain is always homeomorphic to a sphere.
We investigate algorithms for shape extraction that allow the user to have control over the topology of the reconstructed surface and at the same time guarantee high geometric fidelity. We do not only consider binary volumes but also look for generalizations to multi-valued volume datasets.
Also see our papers:
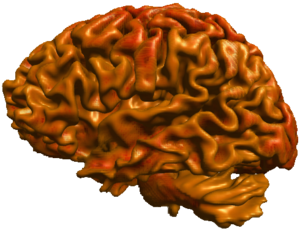
Direct volume rendering algorithms often suffer from occlusion artefacts, e.g. when a certain region of interest like the cerebral cortex is occluded by other regions like the cranial bone. However, their advantage is that they allow to compute visualizations of the 3D image in a flexible and efficient way. On the other hand, surfaces which are extracted to be used for indirect visualization methods have a well defined geometry and therefore can be used for generating lighting and shadow computations. However, isosurfaces might be made of multiple connected components, too, and thus occlusions might also occur in this case.
An alternative approach is based on a re-labeling of the input volume's set of isosurfaces which allows the user to peel off the outer layers and to distinguish unconnected voxel components which happen to have the same voxel values. We use these new labels to mask out certain components and render the original data directly. The masking process is implemented on the GPU which enables interactive frame rates even when the selection of the user changes dynamically. The integration of lighting and shadows is also possible and clearly enhances the 3D impression of the image.
![]()
The digitization of 3D human motion data plays a central role in a variety of applications, such as immersive interfaces for virtual environments, motion analysis in medical contexts, or character animation in movies or games. The process of capturing and processing motion data is a computationally complex task which usually requires a significant amount of manual pre- and post-processing even for established techniques such as optical motion capture systems. This necessity for expert knowledge makes current motion capturing techniques too inflexible in many potential application scenarios.
In this project we develop techniques to support the use of motion capture as a general, flexible input device without the above mentioned restrictions. We implement a self-calibrating framework for optical motion capture, enabling the reconstruction and tracking of arbitrary articulated objects in real-time. Our method automatically estimates relevant model parameters on-the-fly without any information on the initial tracking setup or the distribution of optical markers, and computes the geometry and topology of multiple tracked skeletons.
Also see our papers:

